We find out how to build an efficient portfolio using Nobel Prize-winning methodology and discover that an efficient portfolio is the best possible portfolio.
The problem
Let's identify all of the securities we would consider suitable to hold in an investment portfolio. One way to do this is to start with all the securities in the world and apply screening criteria. For example, from the set of all securities keep only those that are publicly traded, highly liquid, well-regulated and whose market capitalization exceeds some threshold. There are many reasonable screening criteria we can apply, but whatever criteria we do apply, we would likely end up with tens of thousands of stocks, bonds and funds from all regions of the globe. We represent these securities in return-risk space in Figure 1.
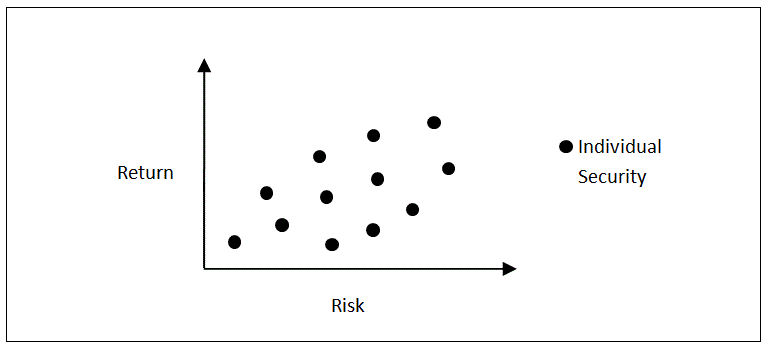
Given this multitude of available securities, how do we build the best possible portfolio? This is one of the most challenging problems in all of financial economics
The solution
The solution is provided by the Nobel Prize-winning diversification theory of the economist Harry Markowitz.[1], [2]. The essence of his theory is that when securities are combined in a portfolio, their risks partially offset each other but their returns do not. More precisely, a portfolio’s return is the weighted average return of its constituent securities whereas the portfolio’s risk is less than the weighted average risk of its constituents—this is often referred to as the only free lunch in financial economics. Therefore, by carefully combining securities, a portfolio can be constructed for any targeted investment return that has the lowest risk of any portfolio which offers the same return. And when we repeat this process for many return targets we obtain a pairing between returns and the lowest-risk portfolios that offer those returns. The collection of these return-risk pairs, called the efficient frontier, is plotted in Figure 2.
All the portfolios that lie on the efficient frontier are called efficient portfolios. Efficient portfolios provide the best risk-return combinations—they produce the lowest risk for a targeted return, or equivalently, the highest return for a target level of risk—and are thus candidates for the ‘best possible’, or optimal portfolio. Notice that all the individual securities lie inside the frontier. This tells us no portfolio of individual securities is optimal and illustrates the principle of diversification: diversifying investments leads to portfolios with higher returns and lower risk.
The development of diversification theory and the efficient frontier has permanently changed the portfolio management environment and its significance cannot be overstated.
Conclusion
We started with a large universe of securities and considered the problem of building an optimal portfolio. Guided by Nobel Prize-winning diversification theory we constructed the efficient frontier. Portfolios on the frontier are optimal, delivering the highest return for a given level of risk. All that remains for us to do is to select a level of risk that is compatible with the investor’s requirements.
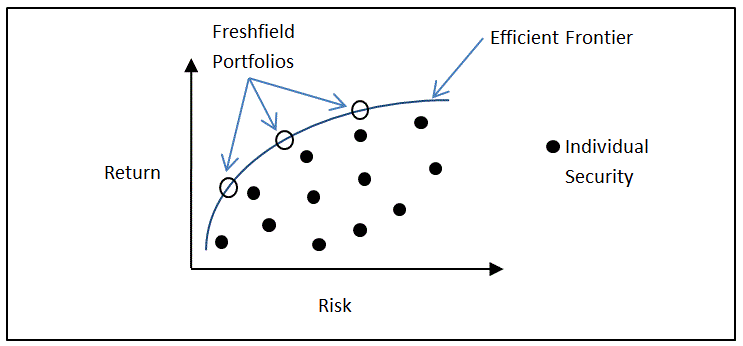
Freshfield builds efficient portfolios for our clients. We first ascertain the level of risk which is compatible with a client’s risk aversion and then build a portfolio on the efficient frontier that corresponds to that level of risk. See Figure 3.
Dr. Andy Lawson is the principal of Freshfield Investments, a Registered Investment Advisory firm in Plano, Texas serving clients locally and nationwide. Freshfield provides investment management and financial planning as a fee-only, fiduciary. To book a virtual or in-person complimentary consultation, please visit our Contact page.
[1] Harry M. Markowitz, The Sveriges Riksbank Prize in Economic Sciences in Memory of Alfred Nobel 1990
[2] Markowitz, H.M. (March 1952). "Portfolio Selection". The Journal of Finance. 7 (1): 77–91.